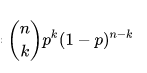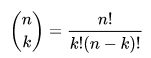If i have an expected winrate of 50% playing a certain game, liken to flipping a coin since all circumstances will be same for later games. Whats the lower bounds and upper bounds of possible winrates over lets say 50 games, 200 games, 500 games, 1000 games?
Anyone that can easily work that out here? I’m sure i could have like 12 years ago but not now it seems.
?
It’s possible to win them all or lose them all. I guess I’m being really thick here in not understanding what you’re asking.
you can use stats to figure out that say X% of the outcomes would fall within these bounds over a specific sample depending on how many standard deviations you use.
As the sample size increases, its likelier to be closer to 50%. Smaller the sample, higher the variance, just like poker so i figured someone here might be able to actually work out the numbers.
Monsieur Pascal had a mighty good triangle back in the day.
Is this what you are trying to find out?
Margins of Error for Coin Flipping
For the bell curve (or normal distribution), the probabilities are represented by the area under the graph. So, to figure out what will happen “19 times out of 20” (i.e., 95% of the time), we just have to figure out how large an interval is required to include 95% of the area under the graph. For a “standard-sized” (unit) normal distribution, the required interval goes from -196% to +196%:!
[[Probabilities when flipping 1000 coins]]http://probability.ca/jeff/writing/bellmarg.pngFor coin flipping, a bit of math shows that the fraction of heads has a “standard deviation” equal to one divided by twice the square root of the number of samples, i.e. to 1/2√n. So, to figure out the margin of error for the fraction of heads when flipping n coins, we simply have to multiply the above 196% by this standard deviation, to obtain the value 98%/√n, i.e. 98% divided the square root of the number of samples.
The conclusion is the following. If you flip n coins, then 95% of the time (i.e., 19 times out of 20), your fraction of heads will be within 98%/√n of the “true” answer of 50%. That is, it will be between 50% − 98%/√n, and 50% + 98%/√n.
For example, with n=10 samples, this margin of error is about 30%, so 19 times out of 20, the fraction of heads will be between 20% and 80%. Or, with n=100 samples, this margin of error is about 10%, so 19 times out of 20, the fraction of heads will be between 40% and 60%. Or, with n=400 samples, this margin of error is about 5%, so 19 times out of 20, the fraction of heads will be between 45% and 55%. Or, with n=1,000 samples, this margin of error is about 3%, so 19 times out of 20, the fraction of heads will be between 47% and 53%. Or, with n=4,000 samples, this margin of error is about 1.5%, so 19 times out of 20, the fraction of heads will be between 48.5% and 51.5%. Or, with n=10,000 samples, this margin of error is about 1%, so 19 times out of 20, the fraction of heads will be between 49% and 51%. And so on.
pretty much yep, thanks!
I think you want
where
which is the probability of getting k successes in n trials if each trial has a probability of p.
