68
I take back what I said about game theory. 62 crushes something like 82, but 63 beats 62 and 64 beats 63 etc up until like 97.
This is 63 vs everything. It lost against everything between 48 and 71, but they were all very close.
from random import randrange
trials = 1000000
def get_score(player_stop_at):
first_roll = randrange(1,101)
if first_roll > player_stop_at:
return first_roll
else:
return randrange(1,101)
def play(a_stop, b_stop):
a_wins = 0
b_wins = 0
for i in range(0, trials):
if get_score(a_stop) > get_score(b_stop):
a_wins += 1
else:
b_wins += 1
print(f'a won {a_wins} with {a_stop} and b won {b_wins} with {b_stop}')
for i in range(1, 101):
play(63, i)
Interesting results microbet. I’m not good enough at understanding python code to figure out where the error lies, but clearly something is up either in your simulation or in my/d10’s excel spreadsheets.
One big surface difference is that yours doesn’t account for ties, but it seems to me that shouldn’t matter, it’s the equivalent of just running it again, and the total equity in my spreadsheet should still match up the same. Hopefully I’m not thinking about that wrong, anyway.
Can you play the game 50 vs 0 and tell me what results you get?
Meaning, stop at 51 vs stop at 1 the way your program is written (I think?)
Yeah…I don’t think any number beats every other number HU. 50 vs 0 in a couple minutes. I changed the code a bit to run everything from 30-80 vs everything from 1-100 with 100k trials each.
50 crushes 1. In 100k trials it was 61772 to 38228
eta: ran it again with 51 instead of 50 and it was a little better.
I’d like to see as close to 62500 as possible for 51 vs 1. I figured this simplest case would be a good way to compare our methods.
That Total Equity in M9 is what I’m looking at, to be clear.
I ran 51 vs 1 again with 10 000 000 trials
a won 6160749 with 51 and b won 3839251 with 1
I’ll quit spamming the thread…and Fabian we can chat separately…but I did another program that ran player one through all numbers from 1 to 100 and for each of those played against a player for each number from 1 to 100 and counted the number of wins the first player got - so each would be a max of 100 if they beat everyone. No one got more than 86 wins and that was with 59 as their stopping point.
eta: that was only 10k trials, trying again with 100k and peak was 59 and 60 with 81 wins. But there are still picks that reliably beat 59 or 60. Nothing is unexploitable I think.
It seems to me that this result doesn’t hold up, and that my spreadsheet and your code are playing subtly different games.
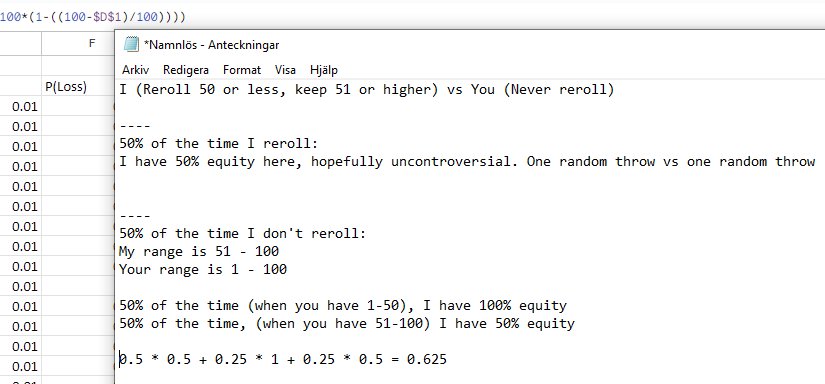
Sorry about the image spam, but I think this case really should be 62.5% equity and nothing else, hopefully that notepad math makes sense.
Surely we can find an analytical solution to this instead of spreadsheeting it.
Outcomes like this suggest that the optimal strategy might be to reroll 62 and under plus some fraction of 63.
My answer there was rerolling on a 1 for player b. Without that I get (100k trials)
a won 620694 with 51 and b won 379306 with 0
Ok my apologies for misunderstanding what you were simulating. That still doesn’t seem consistent with the 62.5% that imo should pop out, though.
Yeah, I don’t see what would be wrong with the 62.5. It’s close, I’m going to look at my algorithm for a few - maybe range is off by one number or something.
The difference is ties. If I change the > for wins to >= I get 629789 and 629789 - 620694 = 9095 and half of that is 4547.5 which added to 620694 is 625241.5 = close enough.
eta: That change did shift the other results a bit. The numbers like 58-63 are so close that head to head you aren’t sure who will win with 10000000 trials.