The thread that sucked me into 2p2 was a CallMeIshmael game theory thread in OOT.
Listen to you
TIL when it comes to math skills I am the chimp of UP.
Anyone want to have an essay writing contest? ![]()
I’ve got the same results using my spreadsheet so if your logic is wrong, we’re both wrong. Interesting that 58 does better than 62. I didn’t try many combinations. I did notice when I was trying to find an iterative equilibrium it oscillated around 62.25 so I guess it’s not surprising that some strategies below 62 could be better. I guess the next step would be to find the winners of other reasonable match ups and see how they relate.
The game theory/equilibrium stuff I’m not as strong on, but those results make intuitive sense to me. 62 (or 62.whatever in the continuous case, I’ve been doing integers only) seems to be game theory optimal strategy where you can’t be exploited from either direction, but when playing against an inferior strategy (50), it makes sense to me that there would be a different strategy (58) that exploits it better.
The oscillation suggests a mixed strategy where where you might be rerolling less than 100% for one number.
If we assume our opponent is standing on >50, the average of such rolls is 75.5 (51+100)/2
If they get less than 50, they re-roll and the average is 50.5 (1+100)/2
Half the time we get 75.5 and half the time we get 50.5 on average.
So the net average is 63.
We can assume on average our opponent will have ~63.
So we should set our number at 63?
But if we’re standing on 63 shouldn’t we assume they will also? They are as smart as us and have the same info.
I’m just assuming the level 0 opponent. As can proven by watching jeopardy, it’s a pretty safe assumption for an unknown.
37% of the time we beat 63 on the first roll
We re-roll 63% of the time. 37% of that time we beat 63.
.63 x .27 is 23.3%
37 + 23.3 is 60.3
So 60.3% of the time we “win”?
Makes sense?![]()
![]()
![]()
Focusing on the average of the die rolls is a bit of a red herring, because the distribution of the results won’t be a nice and symmetrical thing like a uniform or normal distribution in most cases. If the distribution we’re trying to beat were uniform (as is the case if they use the level -1 strategy of "never reroll), then it is just a matter of maximizing your Die EV, it will be the same as maximizing your overall win% of the game, and your overall equity:
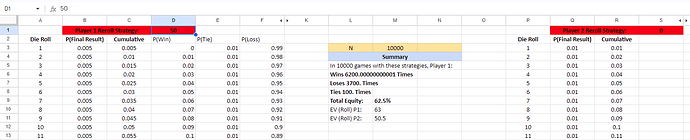
Here, 50 is the best response against a strategy of 0 (because 50 is the highest Die EV strategy available), and the 12.5% of equity you gain is exactly the difference between your Die EV of 63 vs their Die EV of 50.5. If you went with 40 (or 60, same result) here instead, your Die EV would drop to 62.5, and your equity would drop to 62%, and the difference would still be the same. Same is true for any other strategy you could choose.
Once the opponent is playing a level 0 (or higher) strategy of 50, though, the distribution you’re trying to beat ceases to be uniform, and there are now other considerations than pure Die EV. If you know your opponent is using the 50 strategy, the most you can exploit him by is choosing 58 as your reroll number. This gives you an equity of 50.52% in the game. Playing the unexploitable game theory optimal strategy of 62 would still do pretty well, you’d have 50.42% equity in that case:
This is a matter of how you phrase the question, but yes, if you expect your opponent to also solve the game and choose the best strategy, then you will both have to choose the unexploitable strategy of “Reroll 62”, and you’ll end up playing a game with no edge either way. If you think they will go with a different strategy, there’s room for you to choose a different and more exploitative strategy yourself, much like in any poker GTO analogy.
my finger is getting sore from scrolling so hard. i think this deserves to be its own thread
There are two problems here, one small and one big. The small problem (what I tried to explain in the posts above) is that here you’re trying to beat his average of 63, not the actual result of his die roll. While the EV of his die roll is 63, the distribution is not uniform, and so this will introduce some errors, see above.
The much bigger problem though is that here you’re assuming his distribution is exactly 63, every time. You’re trying to beat exactly 63, not “some number he got, the average of which is 63.” The math is basically right though (depends on if you go with 62 or 63 for your own strategy, how do you feel about a guaranteed draw?), I modified my spreadsheet so it always had 63 as the result for Player 2 to show you:
My frequency calc gave a very similar result.
The hard part is their distribution piece. Since we’ve picked a number it’s like are the second team to act in NFL OT. We know what number we want to beat and play accordingly.
Petition to name the thread “Keep rollin’ rollin’ rollin’”
My arm is getting really sore.
Rolling 100 dice at a time is helping.
Imagine if this problem was about taking the sum of five 20-sided die and you could choose to reroll any number of die, keeping the ones you like.
fuck this shit, empiricism is for babies
Instead of being cute I just tried playing the game with “random” numbers. The results of this are unexpected. And you’ll see I ran a million trials of each to get the numbers to settle down as these things are very close. What I’m trying anyway to model here is an actual game instead of expected values where people are choosing stop numbers 1 apart from each other.
# python3
from random import randrange
trials = 1000000
def get_score(player_stop_at):
first_roll = randrange(1,101)
if first_roll > player_stop_at:
return first_roll
else:
return randrange(1,101)
def play(a_stop, b_stop):
a_wins = 0
b_wins = 0
for i in range(0, trials):
if get_score(a_stop) > get_score(b_stop):
a_wins += 1
else:
b_wins += 1
print(f'a won {a_wins} with {a_stop} and b won {b_wins} with {b_stop}')
for i in range(0, 100):
play(i, i+1)