Keeping this one short. (Edit: lol no)
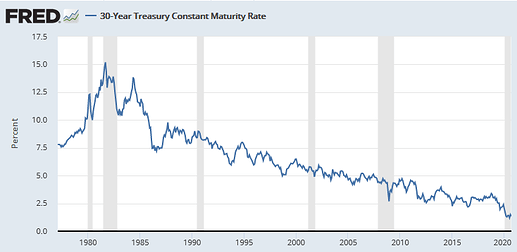
Yes, risk-free rates used to be substantially higher. Here’s the history of 30-year risk-free bond rates since 1980:
Sure, but the Fed is targeting ~2% inflation and they’ve consistently undershot that goal. Moreover, if you believe that risk-free rates are going to increase dramatically, you can (and probably should) just bet directly on that outcome via inflation-protected bonds (TIPS).
Yes, as much fun as it is to dunk on Trump for all the dumb shit he says, he was (accidentally?) right about Fed rates. I think the Fed is and should be an independent entity and therefore not subject to any president’s strong arming. But rates should have been lower during the Obama term.
I’ll try to be briefer and non-repetitive. But, again, the current value of an asset is equal to the present value of its future cash flows. The further in the future a cash flow is, the less it’s worth right now. The easiest way to think about why stock prices go up is that every year that goes by, those future cash flows are getting closer and therefore more valuable. How much more valuable does a future cash flow get each year? By the discount rate used (by the market) to value those future cash flows.
A firm’s stock returns are absolutely not equal to their average earnings growth plus inflation. If you have two firms:
- Firm A, with very high earnings growth
- Firm B, with very low earnings growth
and you discount their future cash flows with the same discount rate, then their change in value each year should be that discount rate. Firm A won’t generate higher stock returns just because it has higher earnings growth. Firm A will have a higher P/E ratio because investors are (correctly) willing to pay more per current dollar of earnings for a higher-growing earnings stream. But over time, both firms (if correctly valued) will generate the same stock returns (i.e., equal to the discount rate used to value them).
Usually when people talk about the risk premium, it means the premium that you’d require to invest in the aggregate stock market, with all of the diversification benefits that you get from owning hundreds/thousands of firms. If you want to invest in individual stocks, you should require a higher rate of return to compensate for your single-stock risk. That means using a higher discount rate.
As for the appropriate risk-free rate, you generally want to use the longest-horizon risk-free asset you can find. So I’d say either the 10-year or 30-year U.S. treasury. Right now, that’s an insanely-low rate of about 1.3%.
What earnings growth rate do you use? This is where things get messy because the 1/(r-g) formula from above assumes a constant rate of growth forever. That’s not a realistic assumption for firms like Apple/Amazon that are experiencing high growth right now - they can’t continue that growth in pepetuity. What you would generally do is use a multi-period model where you estimate realistic growth over the near term, then assume a low “terminal” rate of growth that, mechanically, has to be less than the long-term rate of growth in GDP. (Otherwise, you’d end up forecasting that your individual company would take over the entire economy.)
So for Apple, you might project:
3 years of 15% growth
Another 5 years of 10% growth
8 years of 6% growth
After that, permanent 3% growth
That makes the math a little more complicated, but it’s still pretty trivial to whip up in Excel. (With an 8% discount rate, that series of cash flows would warrant a P/E ratio of 40.) But the key here is that your expected stock return each period is the discount rate you’d use to value those future cash flows - you WILL NOT earn higher stock returns in the first 3 years just because earnings growth is higher.
Note to pedants: This is all complicated by the difference between earnings and free cash flows, the presence of significant non-operating assets, and the effects of dividends/buybacks on projected earnings growth and share count.






 Options are stupid and I’ve swore them off multiple times.
Options are stupid and I’ve swore them off multiple times.