Dice Math Containment Thread

[microbet]

Might have been me. I had a bug where I treated ties incorrectly and the result was looking like 58 or 59. When I fixed it, I was getting the 62/63.

[econophile]

I also reworked my code to account for ties, and I’m now seeing that 62 beats 61 and 63

[Melkerson]

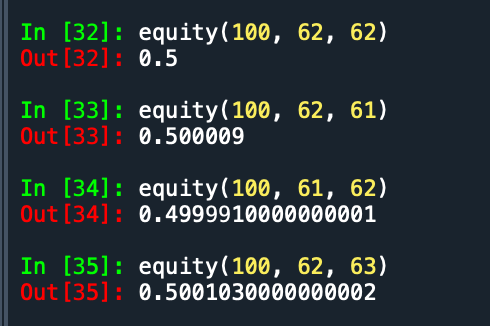
So, what’s the optimal number if you know your opponent is level zero and is staying at >=51. Is it still re-roll 62/stay at 63?

[econophile]

Looks like re-rolling 58 is the highest EV in that case

[eeAWW]

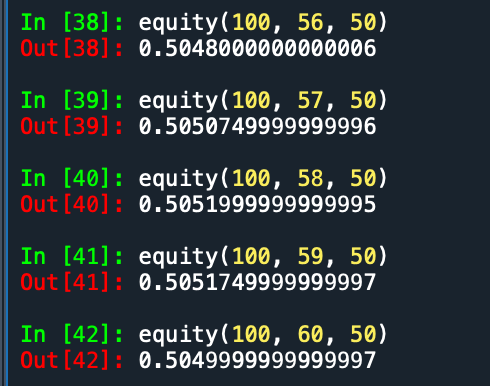
Agreed

[Fabian2]

@Fabian2

I made a spreadsheet where you can change the strategy for both players to play around with different combos:

Not sure what else, if anything, I will do with it yet, but 58 seems to give the best results against an opponent’s level 0 strategy of “Reroll on 50.” 62 vs 50 gives an equity of 50.42%

Melk, having me on ignore never pays off!

[Melkerson]

I knew I saw that somewhere. Just forgot.

[Lawnmower_Man]

It’s just math with an RNG. Well, that plus a lot of (XᵀX)⁻¹XᵀY and sweeping the matrix but you get my point.

[Lawnmower_Man]

@d10

My calculus is on point but my stats is not so great. I have a vivid memory of pissing off my high school stats class by vehemently arguing the wrong side of the Monty Hall problem.

Maybe you can finally come correct by getting on the right sight of the hot hand debate.

[d2_e4]

Oh hai guys. I was directed to this thread by a buddy. So, what’s occurring over here, are you all trying to count? What is the statement of the problem?

[d2_e4]

Judging by the subject of the thread, I should probably tell you that numbers 13 or over are unachievable in a craps roll. Bad times, I know.

[Danspartan]

We have a 100 sided die.

[d2_e4]

That’s a lot of sides, I’m not convinced I know the word for that. Centahedron? Anyway, what are we doing with this die and why?

[d2_e4]

Ok, I mean, I just skimmed the thread and it sounds like you guys have re-discovered the secretary problem. The answer as D–> infinity is 1-1/e. Glad I could help, here all day folks.

[King_of_NY]

This was the original problem that was posted:

@geewhysee

Can any maths nerd help solve an argument? Imagine a game where 2 people roll a D100 and independently choose (without knowledge what the other is doing) whether to keep their roll or reroll it. After the choice the highest number wins.

So the basic strat seems to be reroll 50 or less and stick on 51+ because you are expected to hit a lower roll if you reroll 51. But it doesn’t matter how much you lose by and you know your opponent is likely rerolling 50 or less and keeping 51+ so their average number is going to be higher than 50 (right?)

Should you maximise score EV or go for the win with more extreme variance?

[d2_e4]

Yeah this is the secretary problem.

[Devil]

@d2_e4

the secretary problem

Wiki: Its solution is also known as the 37% rule .

https://x.com/lpachter/status/1779165051460751828

https://x.com/DonMiami3/status/1779259348444987467

dammit @microbet

[d2_e4]

1/e is a transcendental number. Reducing or rounding it to 37% seems so… base.

[Melkerson]

@d2_e4

Yeah this is the secretary problem.

So if I understand the secretary problem correctly, what you’re saying is that if there are 100 secretary applicants, you reject 37 and then take the next one better than best out of the first 37.

Is that right? Doesn’t seem right for some reason.

[d2_e4]

No, You reject everyone who scores below 63, and accept the first applicant who scores above 63.